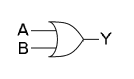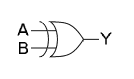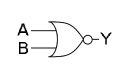데브코스 TIL - CS 파트1
1. 디지털 정보 표현
✅컴퓨터에서 정보의 표현 단위
비트 (bit; binary digit)
- 컴퓨터에서 디지털회로의 조합으로 정보를 표현할 때 이용되는 가장 작은 단위
- 논리적으로 두 가지 중에 하나의 상태를 가지는 것
- 컴퓨터에서 표현하는 모든 정보는 비트를 사용하여 이루어져있음 (이진수)
바이트 (byte)
- 8개의 비트를 모아서 만든 단위
16진수
네 개의 비트를 모아 한 자리로 표현
컴퓨터에서 사용하는 이유는 자릿수 2개를 사용하면 28을 표현할 수 있는데, 28은 곧 1바이트
간단히 1바이트의 값을 2진법을 사용해서 0101 1111 식으로 표기할 게 아니라 그냥 16진법으로 5F16라고 표기해 버리면 많이 축약할 수 있음
✅컴퓨터에서 문자의 표현
문자를 표현하기 위해서는 각 문자에 대응하는 수를 연결하는 표를 이용 (아스키코드)
한글을 표현하는 것은 또 다른 문제
✅컴퓨터에서 데이터 크기 단위
K (kilo)
- 10진법: 103 = 1,000
- 2진법: 210 = 1,024
M (mega)
- 10진법: 106 = 1,000,000
- 2진법: 220 = 1,048,576
G (Giga)
- 10진법: 109 = 1,000,000,000
- 2진법: 230 = 1,073,741,824
2. 이진수로 표현한 정수와 실수
✅ 1의 보수와 2의 보수
1의 보수 (1’s complement)
주어진 이진수의 모든 비트에 대하여 0은 1, 1은 0으로 바꿈
0에 대한 표현이 두가지이므로 2의 보수보다는 불편함
주어진 수 X에 대한 1의 보수
2n - x - 1
0101 + 1010 = 1111
2의 보수 (2’s complement)
주어진 이진수의 1의 보수를 하고난 뒤, 거기에 1를 더함
주어진 수 X에 대한 2의 보수
2n - x
✅ 이진 정수의 표현 범위?
(2의 보수 체계를 이용)
- 가장 작은 수: 1000 0000 =
-128 - 가장 큰 수: 0111 1111 =
127
네 바이트(32비트)를 이용하여 표현할 수 있는 정수의 범위?
231 ~ 231 -1
n 비트를 이용하여 표현할 수 있는 정수의 범위?
2n - 1 2n - 1 -1
✅ 정수가 아닌 수 표현 (실수의 표현 방식)
고정소수점 방식 (fixed-point)
정해진 위치에 소수점이 있는 것으로 간주
부동소수점 방식 (floating-point)
유효숫자와 지수로 나누어 수를 표현
IEEE 754은 가장 널리 쓰이는 표준
부동소수점 연산은 정수 연산에 비하여 시간이 더 걸리고, 정밀도에 한계가 있을 수 있음
3. 컴퓨터 연산 하드웨어
명제와 논리 연산
명제: 놀이기구를 타려면 나이 여섯살 이상, 키 110cm 이상이어야합니다.
나이 >= 6&&키 >= 110
명제: 비가 오지 않는 휴일에는 테니스를 친다
비가 오지 않는다&&휴일이다
✅부울 대수 (boolean algebra)
변수가 가질 수 있는 값은 0 또는 1
명제의 참/거짓에 대응시킬 수 있으며 보통은 1은 참, 0은 거짓으로 간주
연산자
| 구분 | 내용 | 결과 |
|---|---|---|
| 논리역(NOT) | NOT(0) = 1 | NOT(1) = 0 |
| 논리곱(AND) | 1 AND 1 = 1 | 나머지는 0 |
| 논리합(OR) | 0 OR 0 = 0 | 나머지는 1 |
논리 게이트
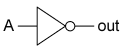
🔍 논리 게이트 NOT
입력 값의 반대되는 값
| x | NOT |
|---|---|
| 0 | 1 |
| 1 | 0 |
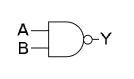
🔍 논리 게이트 AND
두 개의 입력값이 모두 참일 때만 참 아닐 경우 거짓
| x | y | AND |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
🔍 논리 게이트 OR
두 개의 입력값 중 하나만 참이어도 참, 모두 거짓일 경우에만 거짓
| x | y | AND |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
🔍 논리 게이트 XOR
입력값이 두 개가 다르면 1이고, 같으면 0
| x | y | xor |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
🔍 논리 게이트 NAND
AND 출력에 NOT을 붙인 것 (AND 값의 반대값이라고 생각하면 됨)
| x | y | NAND |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
🔍 논리 게이트 NOR
OR 출력에 NOT을 붙인 것 (두 개의 입력이 모두 0일 때만 1)
| x | y | NAND |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
NAND 또는 NOR 게이트만 가지고 모든 회로를 만들 수 있음
✅ 논리식 y= a (b'c)'
💡진리표
| a | b | c | y |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
💡논리게이트
변수의 수 및 논리식이 달라져도 세가지 조합으로 모두 표현이 가능함
✅ 반가산기 (Half Adder)
전 자리올림을 고려하지 않음
💡진리표
| a | b | s | c |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
💡논리식
s = a XOR b
c = a AND b
💡논리 게이트
✅ 전가산기 (Full Adder)
💡진리표
| a | b | ci | s | c0 |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 |
💡논리 게이트
✅ n-bit 가산기 (RCA; Ripple Carry Adder)
비트의 수만큼 배치하고, 맨 아래 자리의 올림을 S로 받아냄
다음 비트는 C로 받아내며, 여러 비트의 가산기를 만듬
※ 컴퓨터는 이러한 가산기보다는 더 좋은 계산기를 가지고 있음 (출력신호가 안정화되는데까지는 시간이 걸리기 때문에)
✅ 가감산기 (Adder-subtractor)
덧셈도 뺄셈도 할 수 있는 계산기
A는 입력,B는 더하거나 뺄 수도 있는 변수- S 신호가
0이면 덧셈을,1이면 뺄셈을 하겠다는 신호
✅ 산술 논리 장치 (ALU; Arithmetic Logic Unit)
컴퓨터에서 쓰이는 산술/논리 연산을 수행하는 회로
CPU의 중요한 부분을 차지
그림출처: 위키백과, 프로그래머스 강의